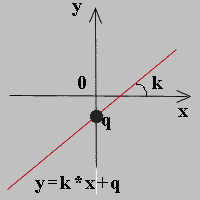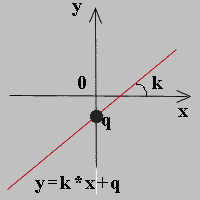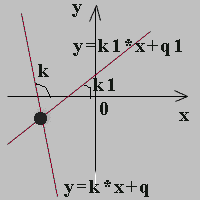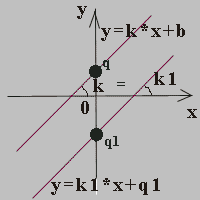Российская академия образования
Институт общего среднего образования РАО
Центр дистанционного образования "Эйдос"
Материалы Всероссийского конкурса "Дистанционный учитель года '99"
http://www.eidos.techno.ru/project/dist_teacher99/
( Поправки на страницу внесены:
)
Дистанционный урок. Математика, класс 9
Тема "Решение систем уравнений первой степени с двумя неизвестными"
1 урок
Тема: "Решение линейных систем уравнений (систем уравнений первой степени) с двумя неизвестными"
(разминка + повторение + теоретические сведения вне школьной программы).
Первый этап - разминка. Время на выполнение - 10 минут.
Можно использовать поисковые системы Интернет.
Ребята и девчата, вспомните имена великих математиков, их высказывания или высказывания о
математике других известных людей и пошлите их в материалы конкурса, воспользовавшись формой,
предложенной на странице
http://users.psu.ru/~samos/samos_2.htm.
Если страница не грузится, то запасной вариант расположен по адресу
http://samosvl.chat.ru/samos_2.htm.
Если вдруг произошло так, что оба адреса на сегодняшний день недоступны, то ответы посылайте
по E-mail school136@pstu.ac.ru.
Второй этап. На второй этап отводится 35 минут.
Из курса математики за 7 класс вы знаете, что имеется несколько способов решения линейных
систем уравнений с двумя переменными: метод сложения, метод подстановки, графический метод.
(Решить систему уравнений - это значит найти такие значения переменных,
при подстановке которых каждое уравнений системы образуется в верное равенство).
Ребята, если Вы плохо помните способы решения линейных систем уравнений, то можете просмотреть
его. Ссылка на повторение
Графический способ решения линейной системы уравнений
Для дальнейшего понятия изложенного материала необходимо повторить графический способ
решения линейной системы уравнений.
Графиком линейного уравнения с двумя переменными, в котором хотя бы один из коэффициентов
при переменных не равен нулю, является прямая.
При решении системы двух линейных уравнений с двумя переменными графическим способом
поступают следующим образом:
- Находят координаты двух каких-либо точек прямой, заданной первым уравнением системы и
строят прямую.
- Находят координаты двух каких-либо точек прямой, заданной вторым уравнением системы и
строят прямую.
- Находят точку пересечения прямых - координаты этой точки удовлетворяют как первому уравнению,
так и второму уравнению, то есть являются решением системы.
ПРИМЕЧАНИЕ:
- Если прямые пересекаются, то система уравнений имеет единственное решение.
- Если прямые параллельны, то система не имеет решений.
- Если прямые совпадают, то система имеет бесконечное множество решений.
Дополнительные сведения к графическому способу:
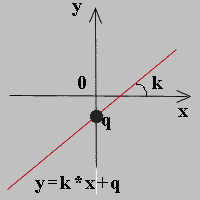 |
Линейное уравнение в системе уравнений имеет вид a*x + b*y = c. Выразим у из этого
уравнения: у = (-a/b)*x - c/b. Обозначим: k = =a/b; q = -c/b. Тогда линейное
уравнение примет вид y = k*x + q, где k - тангенс угла наклона прямой к оси
абсцисс, q - ордината пересечения прямой с осью OY. |
Тогда исходная система линейных уравнений
|
{ |
a1*x + b1*y = c1
a2*x + b2*y = c2 |
может иметь следующий вид:
|
{ |
y = k1*x + q1
y = k2*x + q2 |
Тогда мы можем сделать следующие заключения:
- Прямые пересекаются, если k1 не равно k2 (система уравнений имеет
единственное решение). Значения q1 и q2 могут принимать любые значения.
- Прямые параллельны или совпадают, если k1 = k2.
Прямые параллельны, если k1 = k2 и q1 не равно q2 (система не имеет
решений)
Прямые совпадают, если k1 = k2 и q1 = q2 (система имеет бесконечное множество
решений)
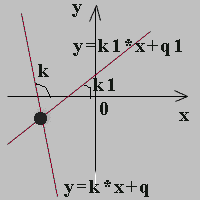 | 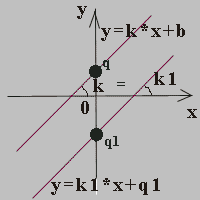 |
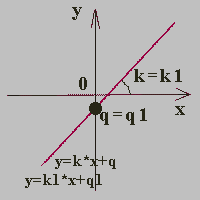 |
прямые персекаются,
система имеет одно решение | прямые параллельны,
решений нет |
прямые совпадают,
система имеет бесконечное
множество решений
|
Вернемся к первоначальным переменным k = =a/b; q = -c/b. Тогда
- Прямые пересекаются, если a1/b1 не равно a2/b2. Значения -c1/b1 и
-c2/b2 могут принимать любые значения (система уравнений имеет единственное решение).
- Прямые параллельны, если a1/b1 = a2/b2 и -c1/b1 не равно -c2/b2 (система не имеет
решений).
- Прямые совпадают, если a1/b1 = a2/b2 и -c1/b1 = -c2/b2(система имеет бесконечное
множество решений).
Данная теория позволяет решать задания следующего типа:
Дана система уравнений
|
{ |
6*x + b1*y = c1
-3*x - 2*y = 5 |
Подобрать коэффициенты b1 и c1 так, чтобы
a) система имела единственное решение (графики прямых пересекались);
b) система не имела решений (графики прямых были параллельны);
c) система имела множество решений (графики прямых совпадали).
Решение.
1) Выразим b1 и c1 через известные коэффициенты системы
a1/b1 = a2/b2 --> b1 = a1*b2/a2 = 6*(-2)/(-3) = 4
-c1/b1 = -c2/b2 --> c1 = b1*c2/b2 = 4*5/(-2) = -10
2) По изложенной теории
a) система имеет единственное решение. (возьмем любое b1, не равное 4, предположим b1=1.
Т.к. с1 может принимать любые значения, то пусть с1=0)
|
{ |
6*x + y = 0
-3*x - 2*y = 5 |
b) система не имеет решений (b1 = 4, с1 не равно -10, пусть с1 = 5)
|
{ |
6*x + 4*y = 5
-3*x - 2*y = 5 |
c) система имеет множество решений (b1 = 4, c1 = -10)
|
{ |
6*x + 4*y = -10
-3*x - 2*y = 5 |
Исходя из изложенной теории и приведенного примера можно сделать другой,
более простой способ определения количества решений системы уравнений, основанный на
пропорциональности коэффициентов при неизвестных и свободных членов.
Задание учащимся. Попробуйте самостоятельно сделать правила
определения количества решений системы уравнений, основанный на пропорциональности коэффициентов
при неизвестных и свободных членов.
Результат пошлите в материалы конкурса,
воспользовавшись формой, предложенной на странице
http://users.psu.ru/~samos/samos_2.htm.
Если страница не грузится, то запасной вариант расположен по адресу
http://samosvl.chat.ru/samos_2.htm.
Если вдруг произошло так, что оба адреса на сегодняшний день недоступны, то ответы посылайте
по E-mail school136@pstu.ac.ru.
Решение систем уравнений с использованием формул Крамера (метод Крамера)
Решения для некоторых систем уравнений можно получать быстрее, используя раз навсегда выведенные
общие формулы в XVII веке в период возникновения и развития теории определителей.
Для системы уравнений из двух уравнений с двумя неизвестными
|
{ |
a1*x + b1*y = c1
a2*x + b2*y = c2 |
выражения D = a1*b2 - a2*b1 ; D1 = c1*b2 - c2*b1 ; D2 = a1*c2 - a2*c1
называют определителями второго порядка. Каждый их них принято записывать
символически в виде матрицы (квадратной таблицы):
Значения определителей находится крестообразным умножением элементов, расположенных по
диагоналям, и последующим вычитанием одного произведения из другого
| D= |
| |
a1 b1
a2 b2 |
| | = a1*b2 - a2*b1 |
| D= |
| |
с1 b1
c2 b2 |
| | = c1*b2 - c2*b1 |
| D= |
| |
a2 c1
a2 c2 |
| | = a1*c2 - a2*c1 |
Решение системы уравнений, с помощью введенных обозначений, имеет вид
x = D1 / D и y = D2 / D
Если D равно нулю, а D1 и D2 не равны нулю, то система не имеет решений.
Если D равно нулю и D1 и D2 равны нулю, то система имеет множество решений.
Если D не равно нулю, то система имеет единственное решение.
Примеры:
| 1 |
{ |
x + 2*y = 3
-x + 2*y = -3 |
Решение.
Формулы для решения системы
D = a1*b2 - a2*b1 ;
D1 = c1*b2 - c2*b1 ;
D2 = a1*c2 - a2*c1 ;
x = D1 / D ;
y = D2 / D | Решение примера
D = 1*2 - (-1)*2 = 4 ;
D1 = 3*2 - (-3)*2 = 12 ;
D2 = 1*(-3) - (-1)*3 = 0;
x = 12/4 = 3 ;
y = 0/4 = 0. |
Ответ: x=3, y=0.
| 2 |
{ |
3x + 2y = 1
6x + 4y = 2 |
Решение.
Формулы для решения системы
D = a1*b2 - a2*b1 ;
D1 = c1*b2 - c2*b1 ;
D2 = a1*c2 - a2*c1 ;
x = D1 / D ;
y = D2 / D | Решение примера
D = 3*4 - 6*2 = 0 ;
D1 = 1*4 - 2*2 = 0 ;
D2 = 3*2 - 6*1 = 0 |
Ответ: система имеет множество решений.
2 урок
Тема: Тема "Решение систем уравнений первой степени с двумя неизвестными"
(практика + зачет).
(результаты решения практической работы можете выслать, воспользовавшись формой,
предложенной на странице
http://users.psu.ru/~samos/samos_2.htm.
Если страница не грузится, то запасной вариант расположен по адресу
http://samosvl.chat.ru/samos_2.htm.)
Первый этап- практическая работа. (15 минут).
Выполните практические задания для закрепления пройденного материала
1. Введите такие значения b1 и c1, чтобы графики уравнений системы были параллельны. Исходная система имеет вид
|
{ |
- 4*x + b1*y = c1
- 4*x + y = 2 |
2. Введите такие значения b1 и c1, чтобы графики уравнений системы совпадали.
Исходная система имеет вид
|
{ |
4*x + b1*y = c1
- 4*x + 4*y = 4 |
3. Введите такие значения b1 и c1, чтобы графики уравнений системы пересекались.
Исходная система имеет вид
|
{ |
3*x + b1*y = c1
3*x + 3*y = 6 |
4. Используя формулы Крамера, определите количество решений следующих систем
| a) |
{ |
-3*x + y = 3
-3*x - 2*y = -6 |
| b) |
{ |
3*x - 2*y = 0
-3*x - 2*y = -6 |
| c) |
{ |
- 4*x - 4*y = 12
- x - y = 3 |
Второй этап - зачет. Время 20 минут
После 65 минут урока на Web-страницу
http://users.psu.ru/~samos/samos_3.htm
будет выложен контролирующий материал.
Если страница не грузится, то запасной вариант расположен по адресу
http://samosvl.chat.ru/samos_3.htm
Загрузите его и выполните предложенные задания, ответьте на вопросы.
Ответы высылайте в материалы конкурса, воспользовавшись формой, предложенной на странице
http://users.psu.ru/~samos/samos_2.htm
Если страница не грузится, то запасной вариант расположен по адресу
http://samosvl.chat.ru/samos_2.htm
Если вдруг произошло так, что оба адреса на сегодняшний день недоступны, то ответы посылайте
по E-mail school136@pstu.ac.ru
Третий этап - заключительный. 15 минут
Используя поисковые системы Интернет, определить,
кем были при жизни Крамер и Гаусс, когда они жили и какие научные знания имели.
Найденный материал отсылается в материалы конференции. Можно прислать ссылки на соответствующие
материалы.
До свидания, ребята. Спасибо за участие в дистанционном уроке, проходившем в рамках
конкурса "ДИСТАНЦИОННЫЙ УЧИТЕЛЬ ГОДА РОССИИ-99". Желаю успехов в дальнейшей учебе.
© Оргкомитет конкурса "Дистанционный учитель года '99"
http://www.eidos.techno.ru/project/dist_teacher99/
E-mail: eidos@accessnet.ru